1. 문제
2019년 12월 25일… 산타 나라는 금고에 넣어둔 선물을 도둑들에게 빼앗겨버리고 말았다.
올해에는 선물을 지키기 위해 특이한 암호화 방식으로 선물이 들어있는 금고의 비밀번호를 관리한다고 한다.
하지만 도둑 중의 도둑인 당신은 산타 나라의 암호화 방식 설명문, 암호화 키가 대부분 적힌 쪽지, 금고의 비밀번호가 적힌 암호화된 쪽지를 손에 넣을 수 있었다!!
과연 이번에도 당신은 선물을 훔칠 수 있을까?
password.txt
m6US+8OA+WK1Dl2kLc60Kxp2o3ydWPuXbZK2vBOrQEPTSzH6Od6Qn137Ctn7oLqm7Nb2uvb2wHU=
Plain Text
복사
encryption key.txt
K1 = 9e 91 9b b3 3a ef * *
K2 = * * f6 ea 6d 93 7f 22
Plain Text
복사
Santa's cipher.txt
To protect Christmas gifts from thieves, our security manager decided to introduce a new cipher system.
In this system, Blowfish algorithm with ECB mode is used and its initial value is set to 0.
Secret information is included things like the password of the safe.
The details are as follows :
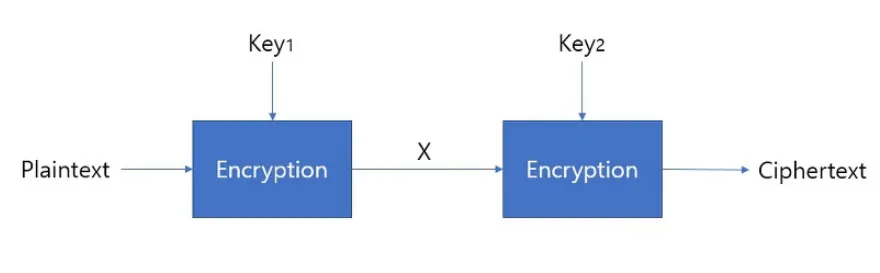
Encryption
1. Prepare randomly generated 8-byte keys, K1, K2.
2. p = base64.decode(plaintext).
3. Perform C1 = Blowfish.encrypt(K1, p).
4. Perform C2 = Blowfish.encrypt(K2, C1).
5. Perform ciphertext = base64.encode(C2).
Decryption
1. Prepare K1, K2.
2. c = base64.decode(ciphertext).
3. Perform D2 = Blowfish.decrypt(K2, c).
4. Perform D1 = Blowfish.decrypt(K1, D2).
5. Perform plaintext = base64.encode(D1).
Here are two examples.
1. plaintext: "QUJDREVGR0g=" ciphertext: "J8LFHyoEuoo="
2. plaintext: "MTIzNDU2Nzg=" ciphertext: "BO9qLlWi45U="
K1 and K2 were secretly sent to all of the santas.
Be careful not to expose the keys.
Plain Text
복사
암호화 및 복호화 로직에 대한 코드가 주어진다. 암호화 알고리즘은 Blowfish 를 사용한다. 현재 사용되는 암호화 키는 k1,k2로 각각 8바이트중 6바이트만 주어진다.
첨에 해당 문제를 풀때는 그냥 무작정 브포를 때렸었다. 4중 포문을 만들고 k1의 6바이트부터 ...
일단 너무 많은 시간이 걸렸고 비교적 많은 사람들이 해당 문제를 푼것으로 보아 이렇게 접근하는것이 아니라고 판단하였다.
롸업을 보니 암호 문제는 안풀어봐서 해당 개념을 몰랐으면 못풀었을 거 같다..
2. 접근방법
Blowfish 알고리즘은 데이터 암호화 표준, 즉 DES와 국제 데이터 암호화 알고리즘을 대신하여 사용되는 암호화 알고리즘이다. 블록 암호 형태로서 해당 알고리즘을 건드리는 것은 아니고 암호화 방식에 따라서 암호 키에 대한 보안성이 결여될 수 있다고 한다.
모든 블록 암호는 Meet in the middle 공격이 가능하다.
문제의 암호화 방식을 보면, 평문을 b64로 디코딩한다음 k1으로 암호화를 진행한다. 그다음 그 결과값을 다시 k2로 암호화를 진행한다.
현재 문제에서 평문 문자열과 암호화된 문자열을 알려준다. "QUJDREVGR0g=" 를 k1으로 암호화를 하면 "X"가 나온다
"QUJDREVGR0g=" ⇒ k1 : "X"
이제 "X" 를 k2로 암호화를 하면 "J8LFHyoEuoo=" 가 나올 것이다. 결국 PlainText와 CipherText를 알고 있기 때문에 Mitm을 진행하여 "X" 에 매칭되는 키 값을 구하면 된다.
3. 풀이
구현 알고리즘은 다음과 같다
1.
k1 하위 2바이트의 모든 경우의 수에 대한 Blowfish 암호화 결과를 저장한다
2.
동일하게 k2 상위 2바이트의 모든 경우의 수에 대한 Blowfish 복호화 결과를 저장한다
3.
1과 2를 비교하여 동일한 값이 있는지 검사한다
4.
동일한 값이 존재하면 그때의 k1,k2 키 값을 얻는다
5.
k1,k2 키를 이용하여 제공된 복호화 방식에 따른 값을 구한다
from Crypto.Cipher import Blowfish
import base64
import binascii
plainT_b64="QUJDREVGR0g="
cipherT_b64="J8LFHyoEuoo="
decode=lambda x:base64.b64decode(x)
#print(decode(plainT_b64))
#print(decode(ciperT_b64))
k1 = bytes.fromhex("9e919bb33aef")
k2 = bytes.fromhex("f6ea6d937f22")
passwd="m6US+8OA+WK1Dl2kLc60Kxp2o3ydWPuXbZK2vBOrQEPTSzH6Od6Qn137Ctn7oLqm7Nb2uvb2wHU="
enc_map=[]
dec_map=[]
def gen_k1_map(key,plain):
c1 = Blowfish.new(key,Blowfish.MODE_ECB)
x = c1.encrypt(plain)
return x
def gen_k2_map(key,cipher):
d1 = Blowfish.new(key,Blowfish.MODE_ECB)
y = d1.decrypt(cipher)
return y
def gen_map(k1,k2,plain,cipher):
global enc_map
global dec_map
for i in range(0xff+1):
for j in range(0xff+1):
value=[]
value.append(chr(i).encode())
value.append(chr(j).encode())
value.append(gen_k1_map(k1+chr(i).encode()+chr(j).encode(),decode(plain)))
enc_map.append(value)
for i in range(0xff+1):
for j in range(0xff+1):
value=[]
value.append(chr(i).encode())
value.append(chr(j).encode())
value.append(gen_k2_map(chr(i).encode()+chr(j).encode()+k2,decode(cipher)))
dec_map.append(value)
def find_key(k1,k2):
global enc_map
global dec_map
for enc in enc_map:
for dec in dec_map:
#print(enc[2],dec[2])
if enc[2]==dec[2]:
k1=k1+enc[0]+enc[1]
k2=dec[0]+dec[1]+k2
print(k1)
print(k2)
return k1,k2
gen_map(k1,k2,plainT_b64,cipherT_b64)
k1,k2=find_key(k1,k2)
d2=Blowfish.new(k2,Blowfish.MODE_ECB)
d1=Blowfish.new(k1,Blowfish.MODE_ECB)
#print(c2)
print(d1.decrypt(d2.decrypt(decode(passwd))))
Python
복사
╭─wogh8732@ubuntu ~/Desktop/ctf/chrismas/phantom
╰─$ python3 ex2.py
b'\x9e\x91\x9b\xb3:\xef-|'
b'l4\xf6\xeam\x93\x7f"'
b'The password of the safe is XMAS{C@tcH_y0u_1F_I_C@N!!!}.'
Python
복사
4. 몰랐던 개념
•
MITM : 네트워크에서 봤던 중간자 공격인줄
•
암호화 방식에 따른 암호키 보안성
•
MITM(Meet in the middle)은 모든 블록 암호 E에 대해
C_2 = E(K_2, E(K_1, plaintext))
Plain Text
복사
일 때,
C_1 = E(K_1, plaintext) = D(K_2, C_2)
Plain Text
복사